二叉树由于非线性,是一种稍稍复杂的数据结构。在本科学习数据结构时基本上时一头雾水,对于二叉树的很多知识都没有理解,考完试以后很快就忘掉了。在后面写代码做题时意识到了数据结构的重要性,于是重新温习,将二叉树的一些常见算法敲一遍。
二叉树基础算法
本次实验环境为Clion+WSL+GCC;用于测试的树如图
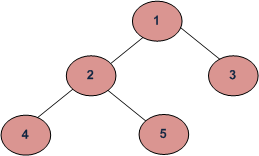
1. 二叉树链式存储结构
首先定义一个二叉树结点的结构体
1
2
3
4
5
6
7
8
9
10
11
12
13
|
//定义节点
struct TreeNode
{
int data;
struct TreeNode *left;
struct TreeNode *right;
//结构体构造函数
TreeNode(int data)
{
this->data=data;
this->left=this->right=nullptr;
}
};
|
2. 二叉树递归遍历(先序、中序、后序)
二叉树的递归遍历是比较容易实现的,主要是要理解层层递归的过程,递归的方法在之后解决问题会经常用到。
1
2
3
4
5
6
7
8
9
|
void preOrder(TreeNode *root)
{
if(root ==nullptr)
return;
cout<<root->data<<" ";
//对左子树和右子树进行递归
preOrder(root->left);
preOrder(root->right);
}
|
1
2
3
4
5
6
7
8
|
void midOrder(TreeNode *root)
{
if(root == nullptr)
return;
midOrder(root->left);
cout<<root->data<<" ";
midOrder(root->right);
}
|
-后序遍历
1
2
3
4
5
6
7
8
|
void postOrder(TreeNode* root)
{
if(root == nullptr)
return;
postOrder(root->left);
postOrder((root->right));
cout<<root->data<<" ";
}
|
递归的代码都比较简洁,主要是弄懂递归的方法。主函数中构造了一个简单的树来进行测试。完整的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
#include <iostream>
using std::endl;
using std::cout;
//定义节点
struct TreeNode
{
int data;
struct TreeNode *left;
struct TreeNode *right;
//结构体构造函数
TreeNode(int data)
{
this->data=data;
this->left=this->right=nullptr;
}
};
void preOrder(TreeNode *root)
{
if(root ==nullptr)
return;
cout<<root->data<<" ";
//对左子树和右子树进行递归
preOrder(root->left);
preOrder(root->right);
}
void midOrder(TreeNode *root)
{
if(root == nullptr)
return;
midOrder(root->left);
cout<<root->data<<" ";
midOrder(root->right);
}
void postOrder(TreeNode* root)
{
if(root == nullptr)
return;
postOrder(root->left);
postOrder((root->right));
cout<<root->data<<" ";
}
int main() {
//测试数据
struct TreeNode *root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
preOrder(root);
cout<<endl;
midOrder(root);
cout<<endl;
postOrder(root);
return 0;
}
|
二叉树遍历非递归实现
虽然递归版本代码简洁容易实现,但是当树的深度比较深时会比较容易发生栈溢出。因此可以自己定义栈或者队列来实现二叉树的遍历。
-
- 弹出栈顶元素
-
- 将弹出元素的右子树入栈
-
- 弹出元素左子树入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
void preOrderWithStack(TreeNode *root)
{
std::stack<TreeNode* > s;
if(root == nullptr)
return;
s.push(root);
while(!s.empty())
{
TreeNode *current=s.top();
s.pop();
cout<<current->data<<" ";
//root节点右孩子先入栈
if(current->right)
s.push(current->right);
if(current->left)
s.push(current->left);
}
}
|
- 中序遍历是二叉树中使用比较多的遍历方法。下面是非递归形式的中序遍历方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
void midOrderWithStack(TreeNode *root)
{
std::stack<TreeNode *> s;
TreeNode *current=root;
while(current != nullptr || s.empty() == false)
{
while(current != nullptr)
{ //左子树节点入栈
s.push(current);
current = current->left;
}
current = s.top();
s.pop();
cout<<current->data<<" ";
current=current->right;
}
}
|
可以看到相对于递归形式是稍微复杂一些。下面来分析一下整个过程。
从整体上看,首先是定义了一个栈,然后有一个大的 while 循环,在这个大循环里还套有一个小循环。整棵树的遍历在这个大循环中完成。在第一次进行小循环时,树的所有左侧结点都会入栈,在这个例 子中,也就是 1 2 4,由于 4 节点没有左右孩子,因此打印该节点的值,依次向上去查找。
- 后序遍历
后续遍历相对来说会麻烦一点。需要用到两个栈来实现。完整的算法流程如下:
- 将root节点压入第一个栈
- 进行循环直到第一个栈空
- 从第一个栈中弹出栈顶节点,压入第二个栈。
- 将上一步弹出的那个节点的左孩子和右孩子压入第一个栈
- 从第二个栈中打印节点
整体算法不算复杂。第一个栈中的存储树节点的顺序称为树的逆后续遍历,通过栈的特性将逆后续遍历在逆一次,就是后序遍历了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
void postOrderWithStack(TreeNode *root)
{
if(root == nullptr)
return;
std::stack<TreeNode* > s1,s2;
s1.push(root);
TreeNode *current=root;
while(!s1.empty())
{
current=s1.top();
s1.pop();
s2.push(current);
//将原来的栈顶节点的左右孩子入栈,要先判断是否为空,否则会访问越界,引发段错误。
if(current->left!= nullptr)
s1.push(current->left);
if(current->right!= nullptr)
s1.push(current->right);
}
while(!s2.empty())
{
current=s2.top();
s2.pop();
cout<<current->data<<" ";
}
}
|
总结
二叉树的遍历是比较基础的算法,在后面做算法题和解决实际问题时会经常用到。所以需要熟练掌握递归和非递归地遍历二叉树,之后才能学习更加复杂地数据结构。
